Let’s face it, folks—mean, median, and mode aren’t just random math terms your teacher threw at you during high school. They’re like the secret sauce to making sense of the world around us. These three amigos of statistics help us interpret data, uncover patterns, and make informed decisions in everyday life. So, whether you’re calculating the average salary in your city or figuring out the most popular ice cream flavor at your local shop, mean, median, and mode are your go-to tools.
Now, before we dive deep into the nitty-gritty, let’s rewind for a sec. Picture this: you’re in a classroom, staring at a whiteboard filled with numbers and formulas. Your teacher is explaining something about central tendencies, and you’re thinking, “What does this even mean?” Well, here’s the deal—mean, median, and mode are all about finding the center of a dataset. But hey, they do it in different ways, and that’s where the magic happens.
Here’s the thing: understanding these concepts isn’t just for math geeks. It’s for anyone who wants to make sense of the numbers that shape our world. From business analysts to sports enthusiasts, everyone relies on mean, median, and mode to connect the dots and draw meaningful conclusions. So, buckle up because we’re about to break it down in a way that’s easy, fun, and oh-so-practical.
Read also:Michael Porter Jr The Rising Star In The Nba Skyline
In this article, we’ll explore the connections between mean, median, and mode, showing you how they work together to paint a clearer picture of data. We’ll also sprinkle in some real-life examples, stats, and insights to keep things interesting. Let’s get started, shall we?
What Are Mean, Median, and Mode Anyway?
Alright, let’s start with the basics. Think of mean, median, and mode as your data BFFs. They’re the trio that helps you make sense of a bunch of numbers. But what exactly are they?
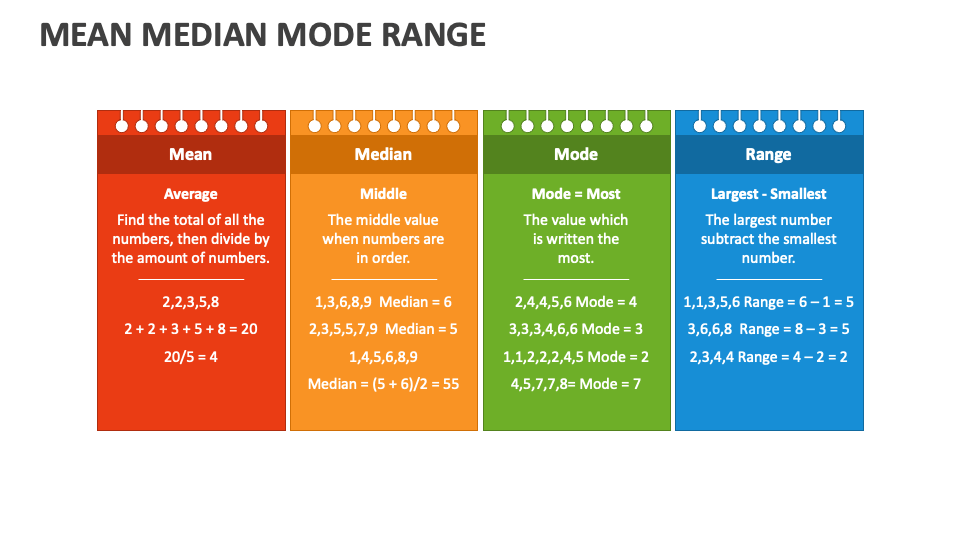
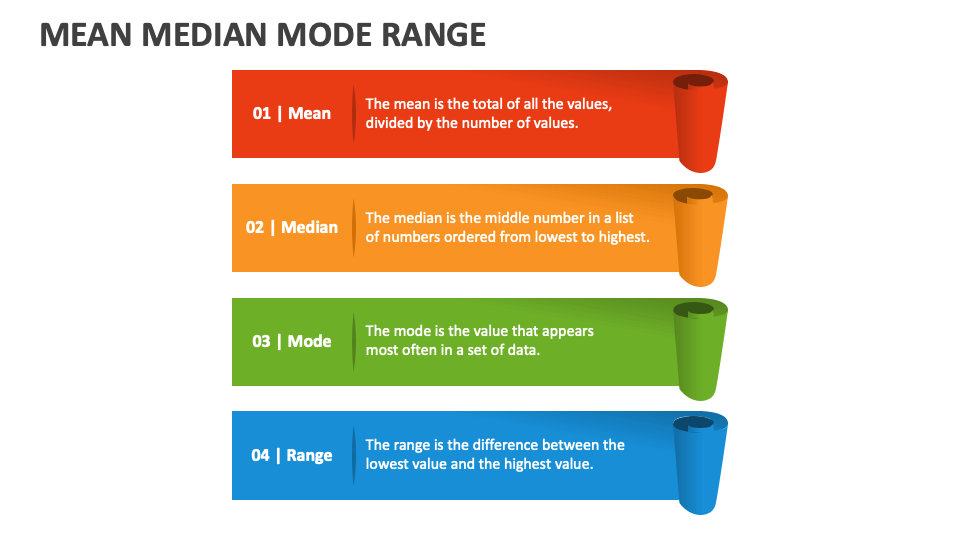
Mean: The Average Joe
The mean is your good ol’ average. You know, the one you calculate by adding up all the numbers in a dataset and then dividing by how many numbers there are. It’s like splitting the total evenly among everyone. For example, if you’ve got the numbers 3, 5, and 7, the mean is (3 + 5 + 7) ÷ 3 = 5. Simple, right? But here’s the catch: the mean can get thrown off by outliers—those pesky numbers that are way higher or lower than the rest.
Median: The Middle Child
Next up, we’ve got the median. This one’s all about finding the middle number in a dataset when it’s arranged in order. If you’ve got an odd number of values, the median is the one right smack in the middle. If you’ve got an even number, you take the average of the two middle numbers. For instance, in the dataset 2, 4, 6, 8, the median is (4 + 6) ÷ 2 = 5. The median is cool because it’s not affected by outliers, making it a reliable measure of central tendency.
Mode: The Popular Kid
Finally, we’ve got the mode. This one’s all about popularity. The mode is the number that shows up the most in a dataset. If no number repeats, then there’s no mode. If two numbers repeat the same number of times, you’ve got a bimodal dataset. And if more than two numbers repeat equally, well, you’ve got a multimodal dataset. For example, in the dataset 1, 2, 2, 3, 4, the mode is 2 because it appears twice.
Why Are Mean Median Mode Connections Important?
Here’s the kicker: mean, median, and mode aren’t just random concepts. They’re interconnected in ways that help us interpret data more effectively. Let’s break it down:
Read also:Where Is American University A Comprehensive Guide To Unlocking Its Location And Prestige
First off, these measures give us different perspectives on the same dataset. The mean tells us the average, the median gives us the middle ground, and the mode highlights the most common value. Together, they paint a fuller picture of what’s going on. For example, in a dataset where the mean is much higher than the median, you might have outliers skewing the average. But if the mean and median are close, the data is likely more evenly distributed.
Real-Life Connections
Let’s talk real life, folks. Say you’re looking at housing prices in your city. The mean price might give you an idea of the overall market, but if there are a few super-expensive homes, the mean could be misleading. That’s where the median comes in handy—it gives you a better sense of what a typical home costs. And if you’re a real estate agent trying to figure out which price range is most popular, the mode’s your best friend.
How to Calculate Mean, Median, and Mode
Now that we’ve got the why out of the way, let’s talk about the how. Calculating mean, median, and mode isn’t rocket science, but it does require a bit of attention to detail. Here’s a quick rundown:
Calculating the Mean
To find the mean, add up all the numbers in your dataset and divide by how many numbers there are. Easy peasy. For example:
- Dataset: 10, 15, 20
- Sum: 10 + 15 + 20 = 45
- Mean: 45 ÷ 3 = 15
Calculating the Median
Finding the median is a bit trickier, but not by much. First, arrange your numbers in order. If you’ve got an odd number of values, the median’s the middle one. If you’ve got an even number, take the average of the two middle numbers. For example:
- Dataset: 3, 7, 9, 12, 15
- Median: 9 (the middle number)
Calculating the Mode
Finding the mode’s super straightforward. Just look for the number that appears the most. If no number repeats, there’s no mode. If two numbers repeat the same number of times, you’ve got a bimodal dataset. For example:
- Dataset: 2, 4, 4, 6, 8
- Mode: 4 (it appears twice)
Applications of Mean Median Mode Connections
Alright, let’s get practical. Mean, median, and mode aren’t just for math class. They’re used in tons of real-world applications. Here are a few examples:
Business and Finance
In the world of business, these measures help analysts understand trends and make predictions. For example, a company might use the mean to calculate average sales, the median to find the typical salary, and the mode to identify the most popular product.
Healthcare
In healthcare, mean, median, and mode help researchers analyze patient data. For instance, the mean might be used to calculate average recovery times, the median to find the typical age of patients, and the mode to identify the most common diagnosis.
Education
In education, these measures help teachers evaluate student performance. The mean might be used to calculate average test scores, the median to find the middle score, and the mode to identify the most common grade.
Challenges in Using Mean Median Mode
Now, let’s talk about the challenges. While mean, median, and mode are powerful tools, they’re not without their limitations. Here are a few things to keep in mind:
Outliers
Outliers can really mess with your mean. A single extreme value can skew the average, making it less representative of the dataset. That’s why the median’s often a better choice when dealing with skewed data.
Missing Data
Missing data can also be a problem. If you’re missing values in your dataset, it can affect the accuracy of your calculations. That’s why it’s important to handle missing data carefully.
Misinterpretation
Finally, there’s the risk of misinterpretation. It’s easy to get caught up in the numbers and forget to consider the context. That’s why it’s important to always interpret mean, median, and mode in light of the bigger picture.
Best Practices for Using Mean Median Mode Connections
So, how do you use mean, median, and mode effectively? Here are a few best practices:
- Always consider the context of your data.
- Use multiple measures to get a fuller picture.
- Be aware of outliers and handle them appropriately.
- Don’t rely on a single measure to draw conclusions.
Real-World Examples of Mean Median Mode Connections
Let’s look at some real-world examples to see how mean, median, and mode work together:
Income Analysis
Income data is a great example of how these measures connect. The mean income might give you an idea of the overall economic situation, but if there are a few super-rich individuals, the mean could be misleading. That’s where the median comes in—it gives you a better sense of what a typical person earns. And if you’re trying to figure out which income bracket is most common, the mode’s your go-to measure.
Test Scores
In education, test scores are another example. The mean score might tell you how well the class performed overall, but the median gives you a better sense of the typical student’s performance. And if you’re trying to identify the most common grade, the mode’s your best bet.
Conclusion: Wrapping It All Up
So, there you have it—the lowdown on mean, median, and mode connections. These measures might seem simple, but they’re powerful tools for making sense of data. Whether you’re analyzing income, test scores, or housing prices, mean, median, and mode help you connect the dots and draw meaningful conclusions.
Now, here’s the deal: if you’ve made it this far, you’re probably wondering how you can put these concepts into practice. My advice? Start small. Pick a dataset that interests you and play around with the numbers. See how the mean, median, and mode interact and what insights they reveal. And don’t forget to share your findings with the world. Who knows? You might just discover something amazing.
So, what are you waiting for? Go out there and start connecting those dots. And if you’ve got any questions or insights to share, drop a comment below. We’d love to hear from you!
Table of Contents
- What Are Mean, Median, and Mode Anyway?
- Why Are Mean Median Mode Connections Important?
- How to Calculate Mean, Median, and Mode
- Applications of Mean Median Mode Connections
- Challenges in Using Mean Median Mode
- Best Practices for Using Mean Median Mode Connections
- Real-World Examples of Mean Median Mode Connections
- Conclusion: Wrapping It All Up